Οριζόντια Πρόσθεση
Όταν θέλω να προσθέσω διψήφιους ή τριψήφιους αριθμούς οριζόντια:
Διαχωρίζω τους αριθμούς σε εκατοντάδες, δεκάδες και μονάδες. Έπειτα προσθέτω τις εκατοντάδες με τις εκατοντάδες, τις δεκάδες με τις δεκάδες και τις μονάδες με τις μονάδες. Τέλος προσθέτω τους αριθμούς.
Πχ: 142 + 356 = ;
100 + 300 = 400
40 + 50 = 90
2 + 6 = 8
-----------------------------
498
Κάθετη Πρόσθεση
Α) Πρόσθεση χωρίς κρατούμενο
Βάζω τον ένα αριθμό κάτω από τον άλλο αριθμό προσέχοντας να είναι οι μονάδες κάτω από τις μονάδες, οι δεκάδες κάτω από τις δεκάδες και οι εκατοντάδες κάτω από τις εκατοντάδες. Στη συνέχεια προσθέτουμε μονάδες με μονάδες, δεκάδες με δεκάδες και εκατοντάδες με εκατοντάδες.
Ε Δ Μ + Ε Δ Μ ---------- |
Πχ: 64 + 25 = ;
- Γράφω την πράξη
6 4
+2 5
--------
και λέω 4+5=9.
- Γράφω το 9 κάτω από τις μονάδες.
- Έπειτα λέω 6+2=8 και γράφω το 8 κάτω από τις δεκάδες.
- Άρα 64+25 μας κάνει 89.
| 6 4 --> πρώτος προσθετέος + 2 5 --> δεύτερος προσθετέος ________ 8 9 --> άθροισμα |
Β) Πρόσθεση με κρατούμενο
Πχ: 69+24= ;
6 9
+ 2 4
--------
9 3
- Προσθέτω τις μονάδες του ενός προσθετέου με τις μονάδες του άλλου προσθετέου: 9+4=13.
- Γράφω το 3 (τις μονάδες) και κρατάω το 1 (δεκάδα), το οποίο ονομάζουμε κρατούμενο
- 1 το κρατούμενο και 6 μας κάνει 7 …. Και 2 μας κάνει 9… οπότε γράφω 9 (στις δεκάδες)
6 9 + 2 4 -------- 9 3 |
Προσοχή όμως! Η πρόσθεσή μου μπορεί να έχει περισσότερα από 1 κρατούμενα. Πχ: 356 + 297= ;
- Τοποθετώ τις Μονάδες κάτω από τις Μονάδες, τις Δεκάδες κάτω από τις Δεκάδες και τις Εκατοντάδες κάτω από τις Εκατοντάδες.
- 6 και 7 μας κάνουν 13. Γράφω το 3 και κρατάω το ένα στο κυκλάκι (κρατούμενο).
- Συνεχίζω. 9 και 5 μας κάνουν 14 ... και 1 το κρατούμενο μας κάνει 15. Σβήνω το κρατούμενο για να μην μπερδεύομαι. Γραφώ το 5 και κρατάω το 1 στο κυκλάκι (κρατούμενο).
- 3 και 2 μας κάνει 5 ... και 1 το κρατούμενο μας κάνει 6. Γράφω το 6. Το άθροισμα (αποτέλεσμα) της πρόσθεσης είναι ο αριθμός 653.
| 3 5 6 + 2 8 7 ----------- | 3 5 6 + 2 8 7 ----------- 3 | 3 5 6 + 2 8 7 ----------- 4 3 | 3 5 6 + 2 8 7 ----------- 6 4 3 |
Αφαίρεση τριψήφιων αριθμών αριθμών
Προσοχή όμως! Η αφαίρεσή μου μπορεί να έχει περισσότερα από 1 κρατούμενα. Πχ: 675 - 289= ;
6 7 5
- 2 8 9
-----------
- Τοποθετώ τις Μονάδες κάτω από τις Μονάδες, τις Δεκάδες κάτω από τις Δεκάδες και τις Εκατοντάδες κάτω από τις Εκατοντάδες.
- 5 βγάζω 9 ... δε γίνεται. Δανείζομαι ένα 1 (μία Δεκάδα) και κρατάω το 1 στο κυκλάκι (κρατούμενο). Το 5 γίνεται 15. 15 βγάζω 9 μας κάνει 6. Γράφω το 6.
- Συνεχίζω. 1 το κρατούμενο και 8 ... μας κάνει 9. Σβήνω το κρατούμενο για να μην μπερδεύομαι. 7 βγάζω 9 δε γίνεται. Δανείζομαι ένα 1 (μία Δεκάδα) και κρατάω το 1 στο κυκλάκι (κρατούμενο). Το 7 γίνεται 17. 17 βγάζω 9 ... μας κάνει 8. Γραφώ το 8.
- 1 το κρατούμενο και 2 ... μας κάνει 3. 6 βγάζω 3 μας κάνει 3. Γράφω το 3. Το αποτέλεσμα της αφαίρεσης (διαφορά) είναι ο αριθμός 386.
| 6 7 5 - 2 8 9 ----------- | 6 7 5 - 2 8 9 ----------- 6 | 6 7 5 - 2 8 9 ----------- 8 6 | 6 7 5 - 2 8 9 ----------- 3 8 6 |
Για να ελέγξω αν το αποτέλεσμα της αφαίρεσης είναι σωστό κάνω την αντίστροφη πράξη. Δηλαδή προσθέτω το αποτέλεσμα που βρήκα (διαφορά) με τον αφαιρετέο της αφαίρεσης. Αν το αποτέλεσμα που βρω είναι ο μειωτέος τότε η πράξη μου είναι σωστή.
Πχ: Για να δω αν η παραπάνω πράξη (675 - 289= 386) που έκανα είναι σωστή, λέω:
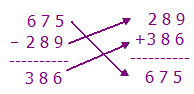
Πηγή: e τάξη
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου